-
Accueil
-
Repères & ressources
-
Son œuvre
-
Pascal savant
- Mathématiques
Les Pensées de Pascal
"Ferox gens nullam esse vitam sine armis rati,
Ils aiment mieux la mort que la paix, les autres aiment mieux la mort que la guerre. Toute opinion peut être préférable à la vie, dont l'amour paraît si fort et si naturel. »
Vanité, (Fragment 63, Sellier)
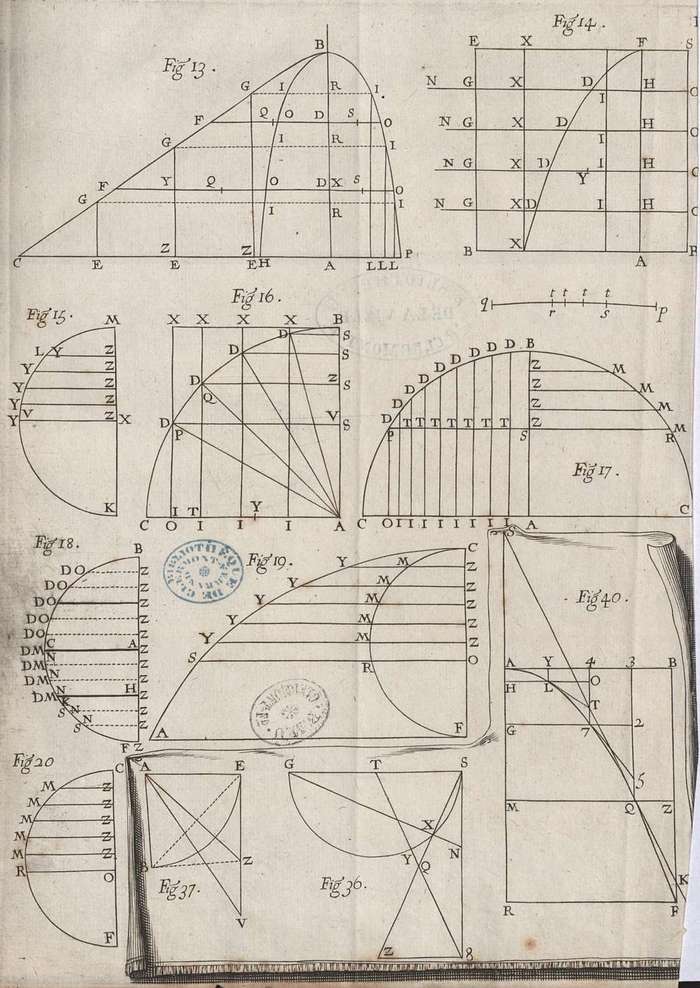
La cycloïde, appelée également roulette, est une courbe définie par la trajectoire d'un point situé sur un cercle roulant sans glisser sur un axe. Blaise Pascal s'y intéresse particulièrement et publie en 1658 son «Histoire de la roulette appelée autrement la trochoïde ou cycloïde, où l'on rapporte par quel degrés on est arrivé à la connaissance de la nature de cette ligne ».
Pascal, Roberval et la quadrature de la cycloïde
Le XVIIème siècle est une période de grand bouleversement scientifique, avec l'émergence du calcul infinitésimal. La cycloïde, qui est une des plus célèbres courbes de cette époque, a été l'objet d'attentions de l'Europe scientifique entière, qui, de près ou de loin, s'est intéressée à cette courbe, qui fut une source inépuisable de validation de méthodes de géométrie différentielle, issues de ce nouvel outil qu'est le calcul différentiel. Dans son "Histoire de la Roulette" de 1658, Pascal souligne l'apport de Roberval sur le calcul de l'aire sous l'arche de cycloïde. La méthode de Roberval est décrite ici dans toute ses audaces et ses imperfections, dont l'emploi des indivisibles de Cavalieri, si difficiles à justifier rigoureusement à cette époque.
La vidéo peut être vue en plusieurs fois :
00:00 Introduction historique
07:15 Qu'est-ce que la cycloïde?
08:55 Tracé de la cycloïde par Roberval
09:53 La construction de la tangente à la cycloïde
13:29 L'expérience de Galilée
14:20 La courbe compagne de la cycloïde
17:06 La méthode des indivisibles
19:30 L'aire sous la cycloïde
Pascal met au point une méthode originale, combinaison d’arithmétique et de géométrie, pour calculer le volume, la surface ou le centre de gravité des solides de révolution engendrés par une courbe. Pour la mettre à l’épreuve, il décide de l’appliquer à la cycloïde, courbe particulière qui a suscité dans un passé récent une vive controverse entre le Français Roberval et l’Italien Torricelli. Pascal institue donc un concours public sur cette courbe, défiant tous les géomètres d’Europe de résoudre les problèmes dont il a lui-même la solution. Le jésuite Antoine de Lalouvère et l’Anglais John Wallis envoient des solutions, qui sont jugées insuffisantes ou erronées. Pascal publie alors ses Lettres de A. Dettonville, qui regroupent ses solutions avec la résolution de quelques problèmes supplémentaires.
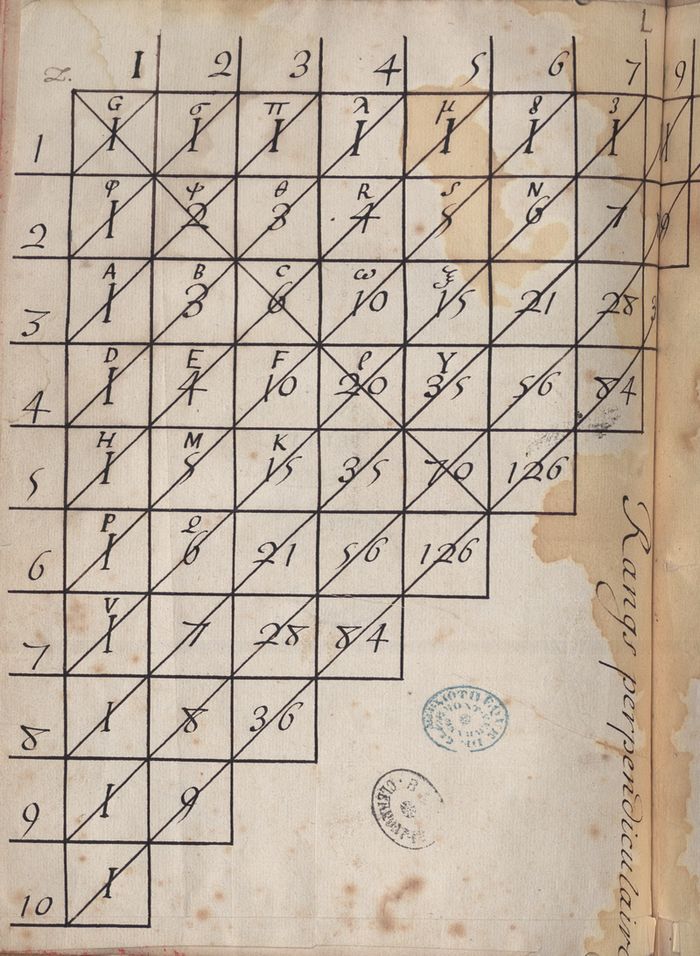
Sur la page 410 du recueil des fragments manuscrits originaux des Pensées apparaît au verso des notes relatives aux Provinciales, un texte mathématique manuscrit, le seul qui nous permette de connaître la manière dont Pascal écrivait les mathématiques. On y remarque que, contrairement à une idée répandue, Pascal disposait d’une manière personnelle de noter ses recherches en termes symboliques. En l’occurrence, il s’agit d’un théorème lié aux Lettres de A. Dettonville sur la cycloïde.
Il s’agit d’un tableau triangulaire de nombres qui se lit de gauche à droite. La première ligne est composée de 1. Les lignes suivantes commencent par 1. Pour construire la suite du triangle, il suffit de faire la somme du chiffre qui se trouve au-dessus avec celui qui se trouve à gauche.
Présentation par M Descotes du triangle arithmétique de Pascal :
|
- triangle_arithmetique |
|
L’utilisation de ce triangle permet la résolution de problèmes de probabilité et trouve des applications dans les jeux de hasard et les combinaisons. Ce triangle n’a pas été inventé par Blaise Pascal. Dès le Xe siècle, diverses formes du triangle arithmétique apparaissent dans de nombreuses civilisations, en Chine, en Inde, dans le monde arabe et en Europe. L'intérêt des mathématiciens de ces diverses contrées pour ce tableau de nombres a des origines diverses mais toutes sont reliées à des problèmes de dénombrement (détermination du nombre d'éléments d'un ensemble), notamment pour calculer ce que l'on appelle aujourd'hui la formule du binôme, c'est-à-dire le développement de (a+b)n. Il semble que ce soit dans les œuvres du mathématicien Al-Karaji (Bagdad, fin du Xe siècle) qu'on trouve la première occurrence d'un développement de cette formule.
Présentation de l'histoire du triangle arithmétique jusqu'au triangle de Blaise Pascal (vidéo du Muséum Henri-Lecoq) :
Dans son Traité du triangle arithmétique publié en 1654, Pascal propose une étude systématique de ce tableau de nombres et démontre 19 propriétés de ce triangle. Un des apports majeurs de Pascal est la présence d'un nouveau type de démonstration d'une propriété portant sur tous les entiers naturels, appelé aujourd'hui raisonnement par récurrence. Depuis, ce tableau de nombres porte le nom de triangle de Pascal.
Les mathématiciens fixent la naissance du calcul des probabilités à l'échange de lettres entre Blaise Pascal et Pierre de Fermat en 1654, au sujet du partage équitable des mises entre 2 puis 3 joueurs s'ils décident d'interrompre une partie en cours. Pascal reprendra la question dans son Traité du triangle arithmétique.
La même année, il adresse à la toute jeune Académie parisienne de mathématiques dirigée par le Père Mersenne un vaste programme de recherche où il annonce « un traité tout à fait nouveau, d'une matière absolument inexplorée jusqu'ici, à savoir la répartition du hasard dans les jeux qui lui sont soumis ; la fortune incertaine y est si bien maîtrisée par l'équité du calcul qu'à chacun des joueurs on assigne toujours exactement ce qui s'accorde avec la justice...Ainsi, joignant la rigueur des démonstrations de la science à l'incertitude du hasard, et conciliant ces choses en apparence contraires, elle peut, tirant son nom des deux, s'arroger à bon droit ce titre stupéfiant : la géométrie du Hasard».
350 ans plus tard, les jeux de hasard tiennent une place importante dans notre société. Ils figurent dans les programmes des lycées car ils utilisent un matériel simple (dés, cartes, roulettes des casinos, sphères du loto) où le nombre d'éventualités est fini.
Nous sommes entourés d'événements aléatoires dont l'étude nécessite l'introduction de l'infini et l'usage de démonstrations par récurrence qui généralisent celles de Pascal.
Focus sur :
Sir Francis Galton (1822-1911), statisticien anglais et cousin de Charles Darwin, invente une planche qui illustre visuellement la convergence d’une loi binomiale vers une loi normale. Le dispositif expérimental matérialise la descente d'une bille qui effectue de haut en bas huit pas au hasard soit vers la droite, soit vers la gauche avec une chance sur deux. Tout se passe comme si ou jouait une partie de Pile ou Face en huit coups. Si on fait chuter 100 billes, elles se répartissent sur les neuf arrivées possibles suivant une courbe en forme de cloche, appelée également courbe de Gauss. Or cette distribution des billes a la même allure que la huitième ligne du triangle arithmétique dont le total est 256 (2 à la puissance 8) et correspond au nombre de chemins que la bille peut prendre : 1 8 28 56 70 56 28 8 1
Si on recommence un grand nombre de fois, on trouvera comme moyenne du nombre de billes pour un total de 100 (en effectuant une règle de trois) : 0,39 3,13 10,94 21,87 27,34 21,87 10,94 3,13 0,39
Une bille a donc peu de chance de tomber aux extrémités (0,39%) de l’arrivée car elle n’a qu’une seule possibilité ou un seul trajet mais a plus de chance de se retrouver au centre du parcours (27,34%) car elle a 70 trajets possibles.
Le triangle arithmétique passionne toujours les chercheurs qui continuent à y découvrir des propriétés remarquables.
La ville de Clermont-Ferrand possède deux originaux de la fameuse machine à calculer inventée et mise au point par Blaise Pascal.
La première, la machine de Marguerite Périer également appelée Machine de Clermont-Ferrand, nous vient en ligne directe de la nièce et filleule de Blaise Pascal. A sa mort, Marguerite Périer la lègue à l’Oratoire de Clermont-Ferrand par testament en date du 4 décembre 1720 « Je leur donne aussy ma machine d’arithmétique inventée par Monsieur Pascal mon oncle, et mesme deux ou trois s’il y en a autant ches moy, lors de mon deceds, et mesme des pièces pour en faire d’autres, s’il s’en trouve ches moy. ». A la Révolution française, le fonds de l’Oratoire devient propriété de la ville de Clermont-Ferrand ; mais certains biens ayant appartenu à Blaise Pascal sont dispersés. Trace est retrouvée de la machine de Marguerite Périer dans une note datée du 1er novembre 1827 et écrite par le bibliothécaire de la ville à cette époque, Benoît Gonod. Plusieurs autres écrits font état de la mobilité de cette machine qui se retrouve au Musée d’histoire et d’art local de Clermont-Ferrand qui deviendra par la suite le Musée du Ranquet. Cette machine, composée d’un caisson en laiton et de baguettes d’ébène, possède 8 roues décimales à l’inscripteur. Elle n’est équipée que d’un seul perfectionnement, la remise à zéro rapide. Sur le devant du caisson, l’écusson porte les armoiries de la famille Pascal surmonté d’un heaume représenté de profil.
La deuxième machine se nomme Machine du Chevalier Durant-Pascal. Son histoire n’est pas aussi claire que celle de la machine de Marguerite Périer. Il semblerait que celle du Chevalier Durant-Pascal ait été initialement donnée à l’Oratoire par Marguerite Périer. A la Révolution, les biens de l’Oratoire ayant été dispersés, le Chevalier Durant-Pascal, cousin de Blaise Pascal, entre en possession de cette machine. Elle reste dans la famille du Chevalier jusqu’en 1985, date à laquelle elle est achetée par la ville de Clermont-Ferrand pour les collections du Musée Du Ranquet. Elle présente la même forme générale, avec l’écusson, que la machine de Marguerite Périer mais elle ne possède que 5 roues à l’inscripteur. Machine en compte monétaire, la roue des unités est en base 12, la roue des dizaines en base 20 puis les suivantes en base 10. C’est le seul exemplaire connu possédant un coffret de transport. De plus, l’étude des chiffres écrits sur les rouleaux du totaliseur montre une particularité du 8 propre à l’écriture d’Etienne Pascal.
Le Musée Du Ranquet ferme ses portes en 2005 et les collections sont confiées aux autres musées de la ville. Le Muséum Henri-Lecoq possédant déjà quelques éléments marquants de l’histoire des sciences, les collections de sciences et techniques lui sont confiées ainsi que les deux machines à calculer de Blaise Pascal.
Il existe d’autres exemplaires connus à travers le monde, trois d’entre eux sont conservés et présentés au Musée des arts et métiers à Paris : la machine de la reine Christine de Suède, la machine du Chancelier Séguier qui a permis à Blaise Pascal d’obtenir un privilège royal protégeant son œuvre et la machine de Louis Périer. Un autre exemplaire se trouve au Musée de mathématiques et de physique de Dresde, en Allemagne, avec 10 roues, la plus longue connue à ce jour. La firme IBM possède également un exemplaire original de la machine de Pascal dans son musée à New York. Le dernier exemplaire connu à ce jour se trouve dans une collection privée : la machine en question fut achetée en 1950 chez un brocanteur comme boite à musique cassée… Ce qui fait un total de 8 machines originales connues à ce jour, sur les nombreux exemplaires et prototypes construits par Blaise Pascal.
Vous pouvez découper et fabriquer la machine arithmétique de Blaise Pascal en téléchargeant ce document : Paper Toy de la machine arithmétique (Muséum Henri-Lecoq).